데이터과학을 위한 통계 리뷰 - 1일차 (탐색적 데이터 분석,분산,편차)
스터디 했던 내용을 바탕으로 재작성 되었습니다.
중요하지 않은 부분은 생략했습니다.
Chapter 1. 탐색적 데이터 분석 (Exploratory data analysis)
(전)통계학 - 추론 : 적은 표본을 가지고 더 큰 모집단에 대한 결론을 도출하기 위한 일련의 복잡한 과정
Tukey, John W. “ The Future Of Data Analysis"(1962)
(후)통계학 - 통계를 공학과 컴퓨터 과학분야에 접목시킴
탐색적 데이터 분석 분야 정립 :Tukey, John W. “Exploratory data analysis "(1977)
Exploratory data analysis is detective work

1.1정형화된 데이터의 요소
-통계적 개념들을 활용하기 위해 가공되지 않은 데이터를 활용 가능한 형태(정형화된 형태)로 변환해야 한다.

-데이터의 분류는 데이터를 분석하고 예측을 모델링할 때 시각화, 해석, 통계 모델 결정 등에 데이터 종류가 중요한 역할을 하기 때문에 꼭 해야 하는 작업이다.
-문자열인지, 범주형인지 분류 시 이점
1.2 테이블 데이터
: 데이터 분석에서 가장 대표적으로 사용되는 객체의 형태. 행과 열로 이루어진 2차원 행렬
1.DataFrame : 가장 기본이 되는 테이블 형태의 데이터 구조
2.Feature : 테이블의 각 열 *유의어 : 특징, 속성, 입력, 예측변수, 변수
3.Record : 테이블의 각 행 *유의어 : 기록값, 사건, 사례, 예제, 관측값, 패턴, 샘플

1.2.2 테이블 형식이 아닌 데이터 구조


1.3 위치추정

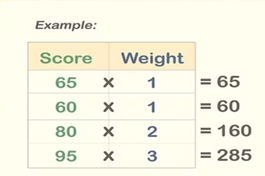



그외 용어정리
가중 중간값 : 가중치의 중간값
로버스트(Robust) : 극단값들에 민감하지 않은 것(머신러닝 모델을 만들다보면 데이터를 정규화하여, 모델에 집어넣기전 입력되는 데이터들이 극단값에 민감하지 않게 반응하게 전처리하여 모델에 집어넣습니다.)
1.4 변이 추정 ~ 1.4.1 표준편차와 관련 추정값들
•변이 : 데이터가 얼마나 밀집해 있는지, 퍼져있는지를 나타내는 정도(산포도)
- 데이터가 어떻게 분포하고 있는지 알고 싶을 때, 확인
- 값이 작을수록 대푯값에 밀집되어 있고, 클수록 멀리 흩어짐
- 두 데이터간의 평균이 같다고 하더라도, 변이에 따라 자료의 내용이나 성질이 달라질 수 있음

변이를 추정하는 다양한 방법
•편차 : 평균으로부터 벗어나 있는 정도. 평균과 데이터의 차이
-> 각각의 데이터 간 편차의 합은 항상 0

•분산 : 편차 제곱의 평균
- 편차는 양수, 음수가 모두 가능하기 때문에, 평균을 계산 할 수가 없음
-> 편차에 제곱을 하여 평균을 구하는 것은 분산
-> 편차에 절댓값을 적용해, 평균을 구하는 것은 평균절대편차
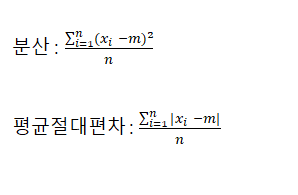
•표준편차 : 분산의 양의 제곱근
- 제곱을 통해 얻은 분산의 값이 너무 크므로, 제곱근을 취해 크기를 줄임

•중위절대편차 : 분산, 표준편차, 평균절대편차 모두 이상치에 민감
- 중간값을 사용하여 편차를 계산
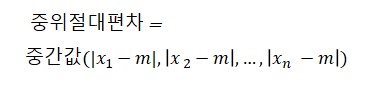
변이 추정 예제


표본분산에서 n-1로 나누는 이유
•통계학에서 모집단에 대한 평균을 구하는 것은 불가능하다고 여김(경제적, 공간적, 시간적 제약)
•표본집단을 통한 해당 모집단의 모수를 추정하는 것이 통계의 목표
•자유도 : 통계치에서 자유롭게 변화시킬 수 있는 변수의 수(독립 변수의 개수)
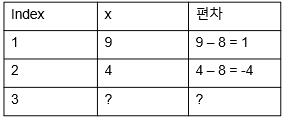
•첫 번째, 두 번째 값이 주어져도, 세 번째 값은 어떤 값이나 올 수 있음

•첫 번째, 두 번째 값이 주어지면 세 번째 값은 고정됨
감사합니다.